MESH & NODAL ANALYSIS

MESH ANALYSIS:

In the mesh analysis, a current is assigned to each window of the network such that the currents complete a closed loop.They are also referred to as loop currents. Each element and branch therefore  will have an independent current. When a branch has two mesh currents, the actual current is given by their algebraic sum. once the currents are assigned, Kirchhoff's voltage law is written for each of the loops to obtain the necessary simultaneous equations.

mesh network

Each mesh produces one equation. These equations are the sum of the voltage drops in a complete loop of the mesh current.^[3] For problems more general than those including current and voltage sources, the voltage drops will be the impedance of the electronic component multiplied by the mesh current in that loop.^[4]

If a voltage source is present within the mesh loop, the voltage at the source is either added or subtracted depending on if it is a voltage drop or a voltage rise in the direction of the mesh current. For a current source that is not contained between two meshes, the mesh current will take the positive or negative value of the current source depending on if the mesh current is in the same or opposite direction of the current source. The following is the same circuit from above with the equations needed to solve for all the currents in the circuit.

${\displaystyle {\begin{cases}{\text{Mesh 1: }}I_{1}=I_{s}\\{\text{Mesh 2: }}-V_{s}+R_{1}(I_{2}-I_{1})+{\frac {1}{sC}}(I_{2}-I_{3})=0\\{\text{Mesh 3: }}{\frac {1}{sC}}(I_{3}-I_{2})+R_{2}(I_{3}-I_{1})+sLI_{3}=0\\\end{cases}}\,}$

Once the equations are found, the system of linear equations can be solved by using any technique to solve linear equations.

Special cases

There are two special cases in mesh current: currents containing a supermesh and currents containing dependent sources.

Supermesh

Figure 2: Circuit with a supermesh. Supermesh occurs because the current source is in between the essential meshes.

A supermesh occurs when a current source is contained between two essential meshes. The circuit is first treated as if the current source is not there. This leads to one equation that incorporates two mesh currents. Once this equation is formed, an equation is needed that relates the two mesh currents with the current source. This will be an equation where the current sourceis equal to one of the mesh currents minus the other. The following is a simple example of dealing with a supermesh.^[2]

${\displaystyle {\begin{cases}{\text{Mesh 1, 2: }}-V_{s}+R_{1}I_{1}+R_{2}I_{2}=0\\{\text{Current source: }}I_{s}=I_{2}-I_{1}\end{cases}}\,}$

Dependent sources

See also: Dependent source

Figure 3: Circuit with dependent source. i_x is the current upon which the dependent source depends.

A dependent source is a current source or voltage source that depends on the voltage or current of another element in the circuit. When a dependent source is contained within an essential mesh, the dependent source should be treated like an independent source. After the mesh equation is formed, a dependent source equation is needed. This equation is generally called a constraint equation. This is an equation that relates the dependent source’s variable to the voltage or current that the source depends on in the circuit. The following is a simple example of a dependent source.

${\displaystyle {\begin{cases}{\text{Mesh 1: }}-V_{s}+R_{1}I_{1}+R_{3}(I_{1}-I_{2})=0\\{\text{Mesh 2: }}R_{2}I_{2}+3I_{x}+R_{3}(I_{2}-I_{1})=0\\{\text{Dependent variable: }}I_{x}=I_{1}-I_{2}\end{cases}}\,}$

NODAL ANALYSIS: 

Typically, electrical networks contains several nodes, where some are simple nodes and some are principal nodes. In the node voltage method , one of the principal nodes is selected as the reference and equations based on KCL are written at the other principal nodes. At each of these other principle nodes, a voltage is assigned, where it is understood that this voltage is with respect to the reference node. These voltage are the unknowns and are determined by nodal analysis.

simple example 

The only unknown voltage in this circuit is V₁. There are three connections to this node and consequently three currents to consider. The direction of the currents in calculations is chosen to be away from the node.

1. Current through resistor R₁: (V₁ - V_S) / R₁
2. Current through resistor R₂: V₁ / R₂
3. Current through current source I_S: -I_S

With Kirchhoff's current law, we get:

${\displaystyle {\frac {V_{1}-V_{S}}{R_{1}}}+{\frac {V_{1}}{R_{2}}}-I_{S}=0}$

This equation can be solved with respect to V₁:

${\displaystyle V_{1}={\frac {\left({\frac {V_{S}}{R1}}+I_{S}\right)}{\left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)}}}$

Finally, the unknown voltage can be solved by substituting numerical values for the symbols. Any unknown currents are easy to calculate after all the voltages in the circuit are known.

${\displaystyle V_{1}={\frac {\left({\frac {5{\text{ V}}}{100\,\Omega }}+20{\text{ mA}}\right)}{\left({\frac {1}{100\,\Omega }}+{\frac {1}{200\,\Omega }}\right)}}={\frac {14}{3}}{\text{ V}}}$

Supernodes

In this circuit, V_A is between two unknown voltages, and is therefore a supernode.

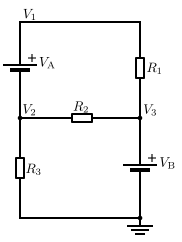
In this circuit, we initially have two unknown voltages, V₁ and V₂. The voltage at V₃ is already known to be V_B because the other terminal of the voltage source is at ground potential.

The current going through voltage source V_A cannot be directly calculated. Therefore, we cannot write the current equations for either V₁ or V₂. However, we know that the same current leaving node V₂ must enter node V₁. Even though the nodes cannot be individually solved, we know that the combined current of these two nodes is zero. This combining of the two nodes is called the supernode technique, and it requires one additional equation: V₁ = V₂ + V_A.

The complete set of equations for this circuit is:

${\displaystyle {\begin{cases}{\frac {V_{1}-V_{\text{B}}}{R_{1}}}+{\frac {V_{2}-V_{\text{B}}}{R_{2}}}+{\frac {V_{2}}{R_{3}}}=0\\V_{1}=V_{2}+V_{\text{A}}\\\end{cases}}}$

By substituting V₁ to the first equation and solving in respect to V₂, we get:

${\displaystyle V_{2}={\frac {(R_{1}+R_{2})R_{3}V_{\text{B}}-R_{2}R_{3}V_{\text{A}}}{(R_{1}+R_{2})R_{3}+R_{1}R_{2}}}}$