What is Volt-Second Balance?

 

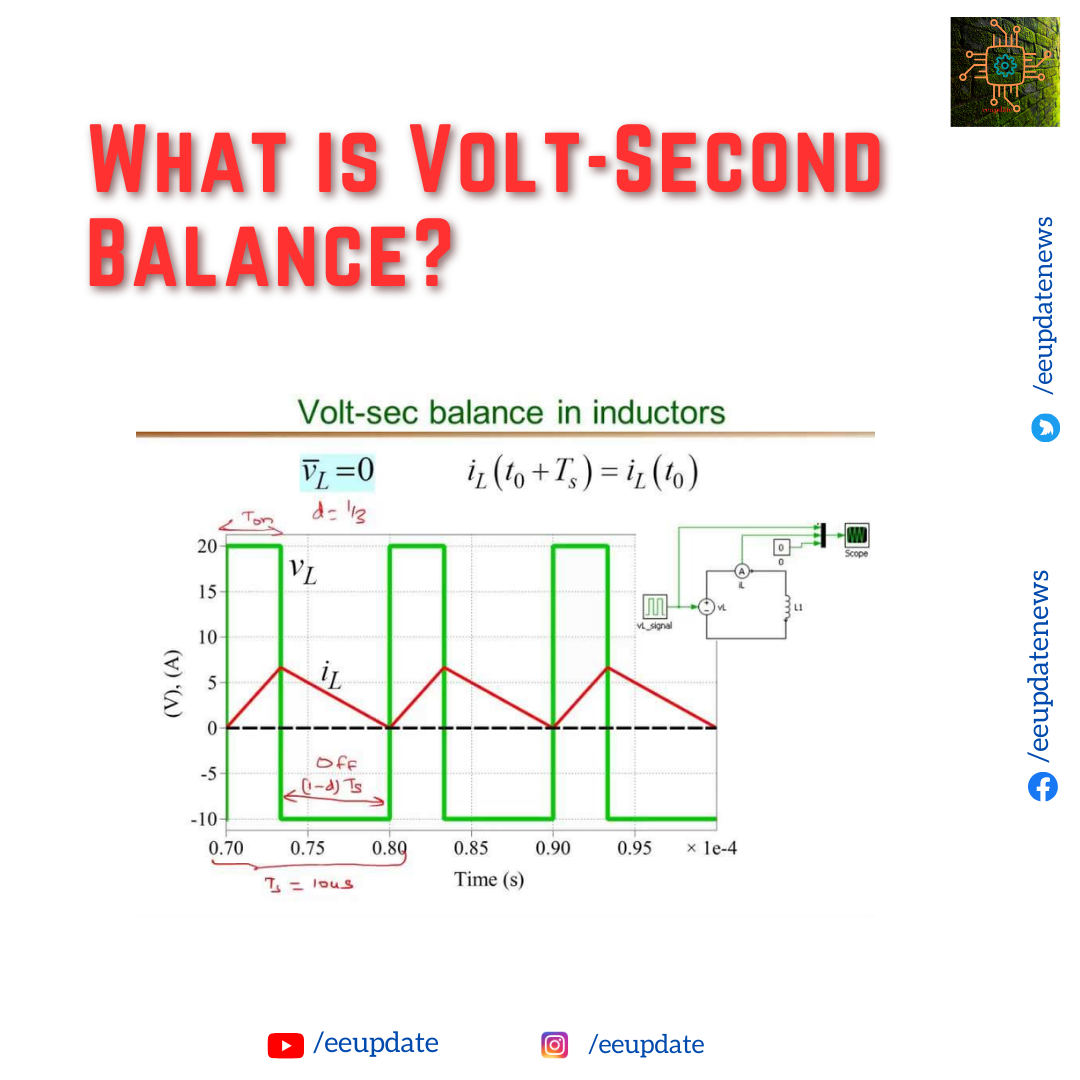
Volt-second balance refers to the principle that the average voltage across an inductor over one complete switching cycle in a steady-state DC-DC converter must be zero. In simpler terms, the energy stored in the inductor during one part of the cycle must equal the energy released during the other part of the cycle to maintain a constant operation.

This principle applies primarily to circuits that use inductors or transformers for energy storage or transfer, including switching regulators and isolated power supplies.

Why is it Important?

Volt-second balance ensures that magnetic components, such as inductors, operate in a stable manner without saturating. If the volt-second balance is violated (i.e., if the voltage applied across the inductor is not balanced over time), the inductor core may saturate, leading to increased losses, overheating, and potentially catastrophic failure of the converter.

Mathematical Explanation of Volt-Second Balance

Let’s break down the concept mathematically to get a clearer understanding.

An inductor follows the relationship:

$$V_L = L \frac{di_L}{dt}$$

Where:

• $V_L$ is the voltage across the inductor
• $L$ is the inductance
• $\frac{di_L}{dt}$ is the rate of change of current through the inductor

This equation shows that the voltage across an inductor is proportional to the rate at which the current through it is changing. When a voltage is applied to the inductor, it causes the current to change, storing energy in the magnetic field. Conversely, when the voltage across the inductor is reversed, the energy stored in the magnetic field is released, changing the current in the opposite direction.

In a switching converter (such as a buck or boost converter), the inductor current ramps up when the switch is closed (because a voltage is applied across it) and ramps down when the switch is open (because a different voltage is applied). To achieve steady-state operation, the net change in inductor current over a full cycle must be zero. This is ensured by balancing the volt-seconds applied during the switch-on and switch-off periods.

Mathematically, the volt-second balance condition for an inductor over a complete switching cycle is given by:

$$\int_0^T V_L(t) dt = 0$$

Where:

• $V_L(t)$ is the time-varying voltage across the inductor during the cycle
• $T$ is the total switching period

This equation implies that the total area under the voltage curve (measured in volt-seconds) over one full cycle must be zero for steady-state operation.

Application of Volt-Second Balance in DC-DC Converters

Volt-second balance is a foundational concept in the operation of various types of DC-DC converters. Let's explore how this principle works in three common types: the buck converter, the boost converter, and the flyback converter.

1. Buck Converter

A buck converter steps down the input voltage to a lower output voltage. Here’s how volt-second balance applies:

• During the "on" period, the switch (MOSFET) is closed, and the input voltage $V_{in}$ is applied across the inductor.
• During the "off" period, the switch is open, and the inductor discharges through the load, with the diode conducting and the inductor voltage equal to $V_{out}$ (but in the opposite direction).

The volt-second balance equation for a buck converter is:

$$(V_{in} - V_{out}) \cdot D \cdot T = - V_{out} \cdot (1 - D) \cdot T$$

Where:

• $V_{in}$ is the input voltage
• $V_{out}$ is the output voltage
• $D$ is the duty cycle (ratio of on-time to total period)
• $T$ is the switching period

Solving this for $V_{out}$, we get:

$$V_{out} = D \cdot V_{in}$$

Thus, the output voltage is directly proportional to the duty cycle, and the converter operates in a stable manner because the volt-second balance condition is met.

2. Boost Converter

A boost converter steps up the input voltage to a higher output voltage. In this case:

• During the "on" period, the switch is closed, and the input voltage $V_{in}$ is applied across the inductor.
• During the "off" period, the switch opens, and the inductor discharges through the load and the diode, transferring stored energy to the output.

The volt-second balance equation for a boost converter is:

$$V_{in} \cdot D \cdot T = (V_{out} - V_{in}) \cdot (1 - D) \cdot T$$

Solving for $V_{out}$, we get:

$$V_{out} = \frac{V_{in}}{1 - D}$$

Here, the output voltage increases as the duty cycle approaches 1. Again, volt-second balance ensures that the inductor operates without saturation.

3. Flyback Converter

The flyback converter is an isolated converter that uses a transformer to store energy in its magnetic core during the "on" phase and transfers that energy to the output during the "off" phase.

The volt-second balance for a flyback transformer is:

$$V_{primary} \cdot D \cdot T = V_{secondary} \cdot (1 - D) \cdot T$$

Where:

• $V_{primary}$ is the voltage across the primary winding
• $V_{secondary}$ is the voltage across the secondary winding
• $D$ is the duty cycle
• $T$ is the switching period

This equation ensures that the transformer core does not saturate, as the magnetic flux in the core is balanced over the switching cycle.

Practical Implications in Circuit Design

1. Preventing Core Saturation: In any inductor or transformer-based design, maintaining volt-second balance is critical to prevent the core from saturating. Saturation leads to increased losses, overheating, and possible failure of the magnetic component.

2. Steady-State Operation: Volt-second balance is essential for ensuring that converters operate in a steady state. Any imbalance can cause instability in the output voltage or current, which may affect the load or other components in the circuit.

3. Control of Output Voltage: The duty cycle is a direct control mechanism for the output voltage in many converters, as seen in the buck and boost converter examples. The volt-second balance helps establish the relationship between input and output voltages based on the duty cycle.

4. Designing Transformer-Based Converters: For isolated converters, such as the flyback converter, volt-second balance is vital to ensure the transformer functions properly and the core does not enter saturation.

Conclusion

The principle of volt-second balance is a fundamental concept in the design and operation of power converters. It governs the behavior of inductors and transformers, ensuring that the energy stored and released during each switching cycle is balanced. Without maintaining volt-second balance, magnetic components would saturate, leading to increased losses and potential damage to the converter.

In designing power electronics circuits, understanding and applying volt-second balance is essential for achieving stable and efficient operation, especially in DC-DC converters where magnetic components play a critical role in energy transfer.