Analog Signal to Digital Signal Conversion

Basic sampling process

 Sampling:          

                    Under certain conditions, a continuous time signal can be completely represented by and recoverable from knowledge of its values, or samples, at points equally spaced in time.This somewhat surprising property follows from a basic result that is referred to as the sampling theorem. This theorem is extremely important and useful.It is exploited, for example, in moving pictures, which consist of a sequence of individual frames,each of which represents an instantaneous view of a continuously changing scene.When these samples are viewed in sequence at a sufficiently fast rate, we perceive an accurate representation of the original continuously moving scene.As another example, printed pictures typically consists of a very fine grid of points, each corresponding to a sample of the spatially continuous scene represented In the picture.If the samples are sufficiently close together, the picture appears to be spatially continuous, although under a magnifying glass its representation in terms of samples become evident. 

              Much of the importance of the sampling theorem also lies in its role as a bridge between continuous time signals and discrete time signals.The fact that under certain conditions a continuous time signal can be completely recovered from a sequence of its samples provides a mechanism for representing a continuous time signal by a discrete time signal.In many contexts,processing discrete time signals is more flexible and is often preferable to processing continuous time signals.This is due in large part to the dramatic development of digital technology over the past few decades, resulting in the availability of inexpensive,lightweight,programmable,and easily reproducible discrete time systems.

                The concept of sampling , then, suggests an extremely attractive and widely employed method for using discrete time system technology to implement continuous time systems and process continuous time signals: we exploit sampling to convert a continuous time signal, process the discrete time signal using discrete time system,and then convert back to continuous time.

Quantization: 

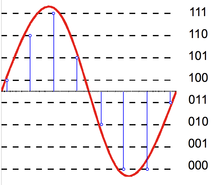Basic quantization process  

In mathematics and digital signal processing, is the process of mapping input values from a large set (often a continuous set) to output values in a (countable) smaller set, often with a finite number of elements.  

 Rounding and truncation are typical examples of quantization processes. Quantization is involved to some degree in nearly all digital signal processing, as the process of representing a signal in digital form ordinarily involves rounding. Quantization also forms the core of essentially all lossy compression algorithms.

The difference between an input value and its quantized value (such as round-off error) is referred to as quantization error. A device or algorithmic function that performs quantization is called a quantizer. An analog-to-digital converter is an example of a quantizer.