Network-INTRODUCTION
A network can be designed by using electric and electronic circuits. so, what should be the definition of an electric and electronic circuit.
Kirchhoff''s voltage law:
Electric circuit is consists of electric elements those are resistors,capacitors,inductors as well as with sources of power.
electronic circuit is composed of individual electronic components, such as resistors, transistors, capacitors, inductors and diodes, connected by conductive wires or traces through which electric current can flow. To be referred to as electronic, rather than electrical, generally at least one active component must be present
so, electric circuit is a part of electronic circuit or device.
The laws defines how the current flows in a circuit and where we get the potential difference in a circuit.those are explained by Kirchhoff''s as below...
Kirchhoff''s current law:
This law is also called Kirchhoff's first law, Kirchhoff's point rule, or Kirchhoff's junction rule (or nodal rule).
This law states that, for any node (junction) in an electrical circuit, the sum of currents flowing into that node is equal to the sum of currents flowing out of that node; or equivalently:
Recalling that current is a signed (positive or negative) quantity reflecting direction towards or away from a node, this principle can be succinctly stated as:
where n is the total number of branches with currents flowing towards or away from the node.
The law is based on the conservation of charge where the charge (measured in coulombs) is the product of the current (in amperes) and the time (in seconds). If the net charge in a region is constant, the KCL will hold on the boundaries of the region. This means that KCL relies on the fact that the net charge in the wires and components is constant.
 |
| KCL rule |
This law is also called Kirchhoff's second law, Kirchhoff's loop (or mesh) rule, and Kirchhoff's second rule.
This law states that
Similarly to KCL, it can be stated as:
Here, n is the total number of voltages measured.
 |
| KVL rule |
Limitations:
KCL and KVL both depend on the lumped element model being applicable to the circuit in question. When the model is not applicable, the laws do not apply. KCL and KVL result from the assumptions of the lumped element model.
KCL is dependent on the assumption that the net charge in any wire, junction or lumped component is constant. Whenever the electric field between parts of the circuit is non-negligible, such as when two wires are capacitively coupled, this may not be the case. This occurs in high-frequency AC circuits, where the lumped element model is no longer applicable.[4] For example, in a transmission line, the charge density in the conductor will constantly be oscillating.
On the other hand, KVL relies on the fact that the action of time-varying magnetic fields are confined to individual components, such as inductors. In reality, the induced electric field produced by an inductor is not confined, but the leaked fields are often negligible.
Example problem:
 |
| example circuit diagram |
Assume an electric network consisting of two voltage sources and three resistors.
According to the first law we have
The second law applied to the closed circuit s1 gives
The second law applied to the closed circuit s2 gives
Thus we get a system of linear equations in :
Which is equivalent to
Assuming
the solution is
has a negative sign, which means that the direction of is opposite to the assumed direction i.e. is directed upwards.



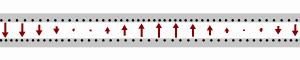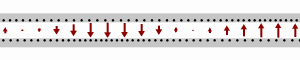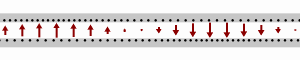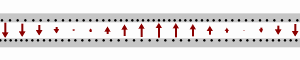








![{\displaystyle {\begin{cases}i_{1}={\frac {1}{1100}}{\text{A}}\\[6pt]i_{2}={\frac {4}{275}}{\text{A}}\\[6pt]i_{3}=-{\frac {3}{220}}{\text{A}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfd39f5713de745cd55eb5f6bcb6d3cc7ba6783c)























No comments