Number Systems
number systems introduction
Decimal number systems:
For example we have a decimal number 8243 which is represented as 8*10^3+2*10^2+4*10^1+3*10^0.
For overall calculation we represent a number in decimal system with constants is,
A3A2A1A0.A-1A-2
representation: A3*10^3+A2*10^2+A1*10^1+A0*10^0.A-1*10^-1+A-2*10^-2
like above we can represent any number in decimal system.
Ex: 123.62
representation in decimal system: (1*10^2+2*10^1+3*10^0).(6*10^-1+2*10^-2)
the decimal number system is said to be of base, radix 10. Because it uses 10 digits and the coefficients are multiplied by powers of 10.
Binary system:
the binary system is a different number system.the coefficients of the binary numbers system have two possible values : 0 and 1. for example, the binary number 110.11 is expressed in terms of base or radix 2.
(110.11)2= (1*2^2+1*2^1+0*2^0).(1*2^-1+1*2^-2)
=(4+2+0).(1/2+1/4)
=(6).(0.5+0.25)
=(6.75)10
*** In general, a number expressed in base r system has coefficients multiplied by powers of r ***
Octal number system:
The radix or base 8 contains the system is known as octal number system.
for example (112)8=(1*8^2+1*8^1+2*8^0)
=(72)10
Hexadecimal number system:
tTe radix or base is 16 for the hexadecimal system.
A-10
B-11
C-12
D-13
E-14
F-15
.
.
.
like this we gave the notation in hexadecimal system.
An example of a hexadecimal number is,
(B65F)16 = (B*16^3+6*16^2+5*16^1+F*16^0)
=(46687)10
This way we have the notations of number systems.

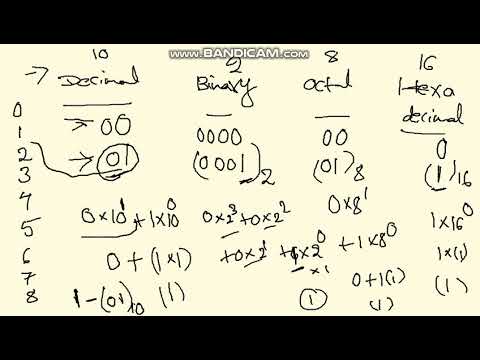






















No comments